
粒度分布の統計計算
粒度分布論、正規分布、対数正規分布、Rosin-Rammlers分布の解説と実例による各種パラメータの計算問題を行うことにより実際問題への応用法を学ぶ。
正規確率紙を配布(用紙は粉体工学会から一枚入手してコピー)
各種の粒度分布式があるが、もっとも情報量が多い対数正規分布に主力をおく。 ここで粒子統計学(Particle Statistics)の出番である。脚注の文献Hatchらの研究を発展させたものである。 テキスト 図1.5の標準正規分布については諸君は統計学で学んできたはずだ。変数をXでなく粒子径 になったのが 式(1.19)、log-log にしたのが、式(1.20)である。 ここで(1.21)式のようにtに置換すれば、標準正規分布になる。 個数分布と質量分布の変換は、式(1.26)これをHatchの式という。 この式の誘導は、式(1.25)の積分である。(この積分は大学受験生程度で可能;ただし大学院生でもかなり苦労する) 得られる情報を下記に板書する。

以上の説明所要時間は約20分、あといきなり問1.6琴引浜問題を解かせる 問題にはないが例題1.6の解答に粒子個数の計算も示してあるから、[個/kg]で答えさせ、提出時に一人一人チェックする。図表の書き方についても指導する。 大部分の学生が時間内に完成する。
個数基準50%径=470.9[μm],'重量基準50%径=507[μm],幾何標準偏差=1.17 体積基準比表面積=4.52[平方メートル /立方m 」, 質量基準比表面積=4.52[ 平方メートル/kg],粒子個数 N=6.17×1000000[個/kg](これを提出時に個別チェックして集めること。なお粒子径は[μm]表示を指導。
地球の赤道半径6378.388[km]として地球一周の粒子重量は、地球一周の粒子総重量13.6[ton] 下記計算のパターンは板書し一部数字を示すとわかりやすい。ふるい網上積算%の意味が具体的に理解できないから。
| 実効目開き | 各ふるい上 | 網上積算 |
| μm | % | % |
| 600 | 0 | 0 |
| 574 | 20.5 | 20.5 |
| 501 | 32.9 | 53.4 |
| 423 | 35.5 | 88.9 |
| 355 | 10.1 | 99.0 |
| 0.1 | 100.0 |
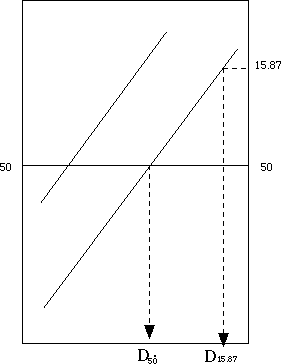
上記程度の略図を板書する。15.87%の意味は確率統計で習っている筈だから説明不要。