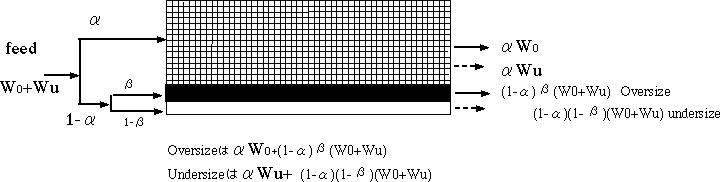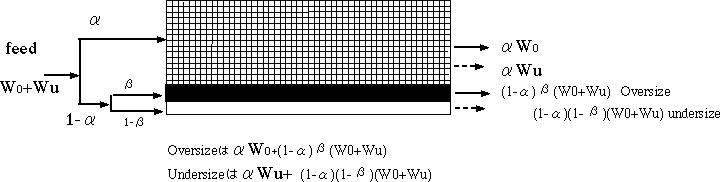
リンク:
総合総合分級効率と 部分分級曲線
一般に分離操作の評価には分離効率が問題になる。
ここではニュートン効率の基本的考え方を、Rietemaの理論を基に図解によって説明してある。
ふるい分けを例にとっているが、成分分離を伴う場合にもそのまま適用できる。
正規確率紙使用(横軸は必ずしもlogをとる必要はない)
p.187-189例題7.1は詳細に解説しているので、ほとんど説明を要しない。
部分分離効率が何かについても一切説明をせず、計算過程で理解する問題。
図7.3(a)(b)(c)をそれぞれ作成しながら考えればよい。分離点を50%分離粒子径にとった場合と、網目開きにとった場合とのNewton効率と効率係数の値の差を追加する。
結構時間がかかるので、大部分宿題になるから、p.185-186を読んで
問7.1の効率係数が常にNewton効率より大きくなる証明を追加する。
問7.1[解] =O/F=1/2 =U/F=1/2 =×=0.25(分離がないのに0.25とは) -=×-(+-1)=(-1)(-1)>0 <1 <1題意通り
総合分離効率についてはテキスト図7.2に図解しているが、もっとも分かりやすいフルイ分けについての下記の図解を追加すると、図7.2を具体的に理解できる。 ここではWの下付のa,bがo,uにしてある。