このポンチ絵は研究中のArcyさんの井戸（計算中に黒板一杯に板書する。必ず太陽を書かせる）流体透過現象の問題
-- Kozeny-Carmanの式 --
このポンチ絵は研究中のArcyさんの井戸（計算中に黒板一杯に板書する。必ず太陽を書かせる）
流体透過現象（Kozeny-Carmanの式）
図3.8の絵を参照しながら流体透過現象が工業操作において重要な役割を果たしていることを理解させる。
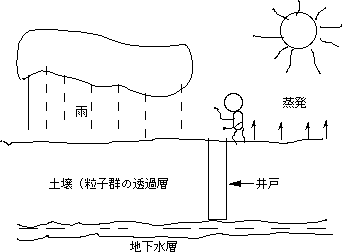
つぎに上の図1を黒板一杯に板書して大地の粉体層を透過する水、井戸掘りから研究が始まったD'Arcyの式（3.49）を示し、それが石油の油井開発に応用されたことをのべ、ダーシーという単位が石油採掘技術で使われていることをのべる。
しかしD'Arcyの式は透過率を実際の地層の試料から実験的に決定するものであった。これから粉体物性から推算する方法の確立までには、長い曲折があった。
人体の心臓の圧力の問題を解くために出たHagen-Poiseuilleハーゲンーポアズイユの式と関連づけるための、Dupitの仮定、動水半径の概念を経て最終的にKozeny-Carmanの式に到達した。
p.75〜78までにその概観が書いてある。仮想の値 、L の説明の図3.9左の図解は誤解を招き易いよくない説明図だと説明し、この斜めの管は曲がりくねっていることを説明しておく。
さて以上の話は科学の発展史であり、（3.57）式のkの値がほぼ5.0に近いというのがこれから計算に使うKozeny-Carmanの式である。
k≒5.0
を確認したCarmanのデータも表3.4に示している。（3.58）または（3.59）の二つの式は化学工学のいろいろな分野で出てくるからここで確実に理解せよと述べる。
このへんで学生はわけが分からなくなって眠くなっているから、カツを入れて「さてこれから数値問題を解け」と図3.10Lea-Nurseの装置（図中毛管長さ280mmの単位が抜けている。当時は長い毛管を使った）と図3.11のBlaineの装置の図を説明する。 以下のLea-Nurseの装置の問題を板書する。
空隙率の計算まで到達するのにいやに手間取る。下の図を板書すれば理解は早い。
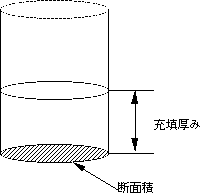
[問題] Lea-Nurseの装置を使ったデータが下記で ある。これから微粉体の比表面積および比表面積球相当径を求めよ。
試料名：シリカ微粉
試料採取量：1.31 [g]
試料充填管断面積：2.0096 [cm^2 ]
試料充填層厚み：0.5 [cm]
気温： 25 ℃
マノメーター液の密度：0.80 [g/cm^3]
圧力差マノメーター液柱の読み：24.2 [cm]
流量： 0.00883 [cm^3/s] [解]
空気粘性係数 0.0001855 [poise] テキスト巻末付表より読取り
空隙率ε=0.50802[-]
体積基準比表面積Sv=71019[cm^2/cm^3]
質量基準比表面積Sw=26799[cm^2/g]
比表面積球相当径Ds=0.845[μm]
計算をせずに文章を書く問題を先に実施するのもよい。
この項については文献を多数年代順に書いているので,理論の発展過程とその応用について小論文にまとめさせる。1839から1930年代までの科学技術史をまとめよと命ずれば,学生はまじめに図解入りの解説を書く。表現力の養成に効果的である。(講義のあと約1時間一杯で全員提出できる。)
問題詳細解答参考値
試料名：シリカ微粉
セル:断面積A=2.0096[cm2]**
空気粘性係数μ=0.0001855[poise]**
空気密度ρ=0.001185[9/cm3］**
試料重量=1.31[9]**
試料層厚み=0.5[cm]**
嵩密度ρＢ=1.30374204[9/cm3]**
圧損△p19.367[gf/cm^2]**
空気流量Q=0.00883[m1/s]
見掛流速 u=0.00439391
a=Δp/(lu)=8812.19841
(ρB/a)^1/3= 0.05777851
粒子密度=2.65[g/cm^3]
空間率 ε=0.50802187
空間率関数=sqrt(ε^3/(1-ε)^2=0.73600001
体積基準比表面積Sv=71019.2421
質量基準比表面積Sw=26799.714
球相当径 Dp=8.4484E-05[cm]
球相当径 Dp=0.84484[μｍ]
**は入力あとは計算値