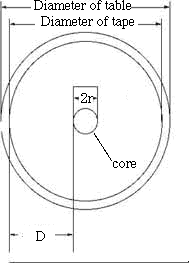
購入した市販の紙テープの直径と芯径(下図のDとd)から次の計算によってもとめま
した。 巻数計算式 は公差d,初項2πr,末項,項数nの等差数列で
r:芯半径[mm],d : 紙厚み[mm],L: テープ全長[m]は次式の等差級数で示 される。
L=2πr+2π(r+d)+2π(r+2d)+2π(r+3d)+・・・+2π{r+(n-1)d }
和 L=n[2πr+2π{r+(n-1)d}]/2=(n/2){4πr+2π(n-1)d}
=πdn^2d+2πrn-nπd ・・・・(1)
これは nの2次式であるから解は
n=- 2πr±sqrt(2πr-4πnπd)/4πd
となるが、D=ndだから(1)式は
πDn+2πrn-πD=L
n巻き分の厚みDは巻いたテープで直接測定できる。
nd=Dを(1)式に入れて
巻数はn=( L+πD)/(πD+2πr)
したがって求めた紙厚みを利用して未知のLの場合の巻厚みが出る。
以上によりテープ全長Lと巻厚みD, 芯径 rを測定すれば、巻数が求められ、
D/nから 紙厚みが求まる。巻数は実際に制作するときの労働の厳しさを示します。こういうのは入学試験問題に出そうですが、出ません。実測値を純粋な数学ではないからです。純粋な数学と実際に直面して考える工学との差が明瞭で面白いことです。同じことは砂時計の寸法計算でもありました。
市販のテープは非常に固く巻かれている。年表製作は人力だから、どこまで締められるかが問題になる。全長46キロを巻く場合はどうなるか。予測のしようがない。そこで予備テストとして白亜紀の3億5000万年までのリールを作って3500メートルの年表を作った。学生に大学の研究室前の廊下で巻かせたが、1週間かかった。十分締めなかったのでだらりとしたみっともない年表になった。「マジメニやれ」とどなることになった。これが丁度NHKの取材があって放送された。
| 色 | 全長[m] | 巻厚み[mm] | n(計算値) | d [mm] |
| 紫 | 250 | |||
| 青 | 500 | |||
| 緑 | 750 | |||
| 黄 | 1000 | |||
| 桃 | 1250 | |||
| 赤 | 1500 | |||
| 白 | 1750 | |||
| 紫 | 2000 | |||
| 青 | 2250 | |||
| 緑 | 2500 | |||
| 黄 | 2750 | |||
| 桃 | 3000 | |||
| 赤 | 3250 | |||
| 白 | 3500 | |||
| 紫 |
さて作業に入ると,カン ブリア紀が終わる前に回転台のベアリングが壊れるハプニングで作業が中断したもの です。メーカーは京都の島津製作所でした。
人類300万年年表,恐竜年表としだいに大きいのを試作した結果,大きくなるほど固 く締まることがわかり,十分固くまいた場合のdの値からD=1.25mと計算しました。試
作した人類300万年年表,恐竜年表もミュージアムに常時展示しています。また人類 300万年年表制作キットも実費販売しています。これ一個あればゆっくり引き出しな
がら,人類あゆみの長さを想う大演説ができます。引き出した七色のテープが机上に 山積みされる様は実にきれいでだれも退屈しません。全部引き出したとき,机からい
まにもこぼれ落ちそうになった人類史の迫力はナルホド,人類の苦難に満ちた長い長 いあゆみへの敬意が込み上げてきます。「ようやく人類最古の女性ルーシーさんにお
会いできましたが,さてこのままでは顎が出っ張った原始人です。たいへんだ。もう いちど巻直しながら現代までもどりましょう。」この往復でたっぷり1時間かかりま
す。(1985年11月27日にNHK市民大学講座で実演しましたが,当時はまだサンドミュー ジアムがなく,ようやく1.4億年の恐竜年表が出来たばかりで,地球46億年テープ年
表は夢物語でしたそれでも1.4キロ,これをまくのに卒論生はふらふらになったもの でした。)
ミュージアムへおでかけの時は,
計算と実際の差がどれくらいか,ぜひお確かめ下さい。
当時,46キロのテープと格闘したコンパニオンもいますから涙の物語を聞くのもいか が。ただし展示パネルに出ている式の誘導は難解で且つミスがあるのでご注意。
